Navigating Uncertainty: A Simplified Guide to the Kalman Filter
Welcome to our exploration of geolocation precision. In this segment of our series, we delve into a foundational tool that has significantly impacted the accuracy of global navigation systems – the Kalman filter. Our focus is on the technical application that underlies its role in geolocation. From its inception to real-world implications, we unravel the Kalman filter's equations and explore its instrumental role in refining the precision of sensor data across diverse industries. Join us on this journey, where we navigate through the nuanced landscapes of geolocation technology and control theory, underpinned by the robust and sophisticated Kalman filter.
What is the Kalman Filter?
At its core, the Kalman Filter is a sophisticated algorithm that excels in scenarios where measurements are imprecise and disturbances abound (Kalman, 1960). Imagine it as a high-tech compass guiding through the complexities of noisy information, ensuring accurate state estimation in real-time.
Trajectory Precision in Space Exploration: A Kalman Filter diagram showcasing the interplay of predictive equations and measurements. This critical tool, developed by Rudolph Kalman, optimized spacecraft positioning during Apollo lunar missions, overcoming challenges posed by non-linear dynamics and intermittent measurements (Trainer, J. How NASA Used the Kalman Filter in the Apollo Program)
How Does it Work?
The Kalman Filter navigates through two key phases - prediction and update - in a continuous loop:
1. Prediction Phase: Looking Forward
The iterative process begins by predicting the current state based on the previous state and the system dynamics. It forecasts where things should be without considering measurements.
2. Update Phase: Blending Measurements and Predictions
Real-world measurements enter the stage, often imperfect and laden with noise. The Kalman Filter intelligently weighs these measurements against its predictions, considering their reliability. Precise measurements wield more influence, while less reliable ones have a diminished impact.
3. Optimal Fusion: Minimizing Uncertainty
The magic happens as the Kalman Filter optimizes the fusion of prediction and measurement. It doesn't blindly accept data; instead, it calculates the optimal blend, minimizing the overall uncertainty in the process.
4. Iterative Refinement: A Continuous Cycle
The process repeats as new measurements come in. The filter continuously refines its estimation, dynamically adjusting to changes in the system and the quality of incoming data.
What is Covariance and why is it important?
Enter the silent conductor: covariance. In the realm of Kalman Filtering, covariance is the measure of how variables move together. For instance, say a tank is filling up with some industrial liquid at a constant rate and has flow meters, temperature sensors, and level sensors attached; the Kalman Filter can discern the reliability of measurements from each sensor from the noise and weights them based on their reliability.
Demystifying Covariance:
Covariance quantifies how variables move together. If positive, they tend to increase or decrease in sync; if negative, one rises as the other falls.
In Kalman Filtering, understanding covariance ensures the algorithm weighs measurements appropriately. It's the assurance that our conductor orchestrates a precise and harmonious symphony of data, even amid variability and uncertainty.
Why does it Matter?
In a world inundated with data, the Kalman Filter's ability to navigate uncertainty with precision is crucial. It's not just about making sense of measurements; it's about seamlessly adapting to changes, filtering through noise, and providing a refined understanding of the system's state.
As we journey through the landscape of artificial intelligence and control theory, the Kalman Filter stands as a testament to the power of algorithms in stabilizing uncertainties in measurements, ensuring our systems have a stable estimation of their current state.
Kalman Gain: The Secret Sauce:
The magic ingredient in the Kalman Filter lies in its ability to intelligently decide, at each interval, which measurements can be trusted more. This process involves calculating what is known as the Kalman Gain (Kalman, 1960).
The Kalman Gain (K) is the crucial element that dictates how much the filter should trust the prediction versus the new measurement. At its essence, the Kalman Gain is a dynamic weighting factor assigned to each measurement. It is determined by the covariance of the predicted state and the covariance of the measurement.
The Formula:
Where:
- K is the Kalman Gain,
is the covariance of the predicted state,
- H is the measurement matrix, and
- is the covariance of the measurement noise.
Decoding the Equation:
1. Prediction Covariance :
This represents how much we trust our prediction. A smaller prediction covariance means we have high confidence in our prediction.
2. Measurement Covariance(R): This represents the reliability of our measurement. A smaller measurement covariance means we have high confidence in our measurement.
3. Measurement Matrix (H): This matrix links the predicted state to the measurement space.
The Decision Process:
1. High Ppred , Low R If our prediction is highly confident (small Ppred) and our measurement reliability is low (large R), the Kalman Gain will be small. In this case, the filter trusts the prediction more and adjusts the current state based on it.
2. Low Ppred , High R: Conversely, if our prediction has high uncertainty and our measurement reliability is high, the Kalman Gain will be large. Now, the filter trusts the measurement more and adjusts the current state accordingly.
Once the Kalman Gain (K) is calculated, the state update in the Kalman Filter involves a weighted fusion of the prediction and the actual measurement. The Kalman Gain acts as a scaling factor, determining how much influence the measurement should have in adjusting the current state. The update equation is given by:
Here's a breakdown of the components in the equation:
The refined estimate of the current state after incorporating the measurement information.
The predicted state was obtained from the previous iteration in the Kalman Filter.
The actual measurement received at the current time.
The measurement matrix which relates the state to the measurement space.
The key steps in the state update process:
1. Residual Calculation:
This term represents the residual or the difference between the actual measurement (Zmeasured) and the predicted measurement (H⋅Xpred). It quantifies how much the prediction deviates from the reality captured by the measurement.
2. Scaling by Kalman Gain:
Here the Kalman Gain (K) acts as a scaling factor, determining the contribution of the residual in updating the state. A high Kalman Gain means the filter trusts the measurement more, while a low Kalman Gain gives more weight to the prediction.
3. Final State Update:
The updated state is obtained by combining the predicted state (Xpred) with the corrective term determined by the Kalman Gain and the residual. This fusion ensures that the filter adapts to the current measurements while maintaining a balance with the predicted state.
4. Iterative Refinement:
The Kalman Filter operates in a continuous cycle of prediction, measurement, and update. As new measurements become available, the filter refines its state estimation iteratively. This dynamic adaptation to changing conditions is what makes the Kalman Filter a powerful tool in real-time applications.
The significance of this process lies in the Kalman Filter's ability to provide accurate and timely state estimations by dynamically adjusting to evolving scenarios, even in the presence of uncertainties.
https://ece.montana.edu/seniordesign/archive/SP14/UnderwaterNavigation/kalman_filter.html
Extended Kalman Filter:
Now, let's delve into the intricacies of the Extended Kalman Filter (EKF), a sophisticated variant of the Kalman filter specifically crafted to navigate the challenges posed by nonlinear systems. To grasp the essence of the EKF, let's first demystify the terms "linearities" and "nonlinearities." In the world of mathematical modeling, a linear system exhibits behaviors that are proportional and additive, making predictions and estimations straightforward. On the other hand, nonlinear systems introduce complexities, showcasing behaviors that don't adhere to these simple rules.
Imagine tracking the trajectory of an object using a radar system. In a linear world, the radar's measurements would directly correlate with the object's position and velocity, forming a predictable relationship. However, nonlinearities may come into play if, for instance, the object undergoes erratic maneuvers, experiences atmospheric disturbances, or encounters irregularities in its path.
This is where the EKF emerges as a powerful ally. In situations where the standard Kalman filter might struggle due to nonlinear dynamics, the EKF excels by skillfully handling these intricacies. The EKF achieves this by employing a clever strategy of linearizing the system at each step, essentially creating a series of linear approximations that collectively provide a reliable estimate of the system's state utilizing a mathematical tool known as a Jacobian matrix
When tackling complex systems, the Jacobian acts as a tool to estimate how a slight change in one variable influences the overall outcome. It's akin to having a guide that reveals the impact of a small adjustment in one direction. In the realm of the Extended Kalman Filter, this guide becomes indispensable for handling the intricacies of non-linear systems. Instead of getting lost in complexity, the Jacobian provides a simplified approximation at each step, allowing for more accurate predictions and adjustments as we navigate the challenges of the real world.
1. Prediction Step:
- Similar to the traditional Kalman filter, the EKF begins with a prediction of the current state based on the previous state and system dynamics. The prediction step involves the following equations:
Here, xk|k-1 is the predicted state, f represents the nonlinear system dynamics, uk-1 is the control input, Pk∣k−1 is the predicted state covariance, Ak−1 is the Jacobian matrix of f, and Qk-1is the process noise covariance.
2. Measurement Update Step:
- In this step, the EKF incorporates real-world measurements, adjusting the predicted state based on measurement data. The equations for the measurement update step are:
In this expression:
K_k represents the Kalman gain at time k.
Pk∣k−1 is the predicted covariance matrix at time k.
Hk is a matrix at time k.
HkT denotes the transpose of matrix Hk.
Rk is a covariance matrix at time k.
(Hk⋅Pk∣k−1⋅HkT+Rk)^−1 represents the inverse of the sum of two matrices.
xk represents the updated state at time k.
xk∣k−1 is the predicted state at time k.
Kk is the Kalman gain at time k.
zk is the measured state at time k.
h(xk∣k−1) is the measurement prediction function.
Here, Kk is the Kalman gain, Hk is the Jacobian matrix of the measurement function h, Rk) is the measurement noise covariance, zk is the actual measurement, xk is the updated state, and Pk∣k is the updated state covariance.
3. Iteration
The EKF iteratively repeats these steps for each time step in the sequence, refining the state estimation based on the evolving system dynamics and incoming measurements.
The strength of the Extended Kalman Filter lies in its ability to handle nonlinearities through the linearization process, ensuring accurate state estimates even in systems with complex and non-linear behaviors. This iterative and adaptive approach makes the EKF a valuable tool in a wide range of applications, from robotics to sensor fusion and geolocation systems.
Solving the UAV Localization Problem Using a Smooth Variable Structure FilteringSolving the UAV Localization Problem Using a Smooth Variable Structure Filtering - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/Extended-Kalman-Filter-Algorithm_fig5_300067587
Real-World Example:
Let's consider a more down-to-earth example to understand how the Kalman filter works in practical terms. Imagine you have a friend who loves tracking their daily steps using a fitness tracker. However, your friend encounters a common issue: the tracker occasionally provides inaccurate step counts due to motion sensor errors or sudden movements.
Enter the Kalman filter as a digital problem-solver. It acts like a smart assistant, helping your friend get more accurate step counts by combining predictions and real-time measurements. Think of it as your friend predicting their step count based on their previous steps and walking speed. Now, when the tracker's sensor data comes in, the Kalman filter dynamically adjusts the prediction, giving more weight to reliable measurements and less to those influenced by sporadic motion or sensor glitches (Bertozzi et al., 2004).
The filter's decision-making process is akin to your friend trusting their tracker's prediction when the data seems consistent but relying more on real-time measurements when the tracker might be acting up. This delicate balance is achieved through a mathematical term called the Kalman gain, which essentially determines how much trust your friend should place in the tracker versus their own prediction.
So, in the end, the Kalman filter helps your friend achieve a more reliable step count, even when dealing with occasional inaccuracies from the tracker. It's a practical tool that enhances the accuracy of everyday technologies we encounter, making our experiences smoother and more dependable.
Airplane Geolocation:
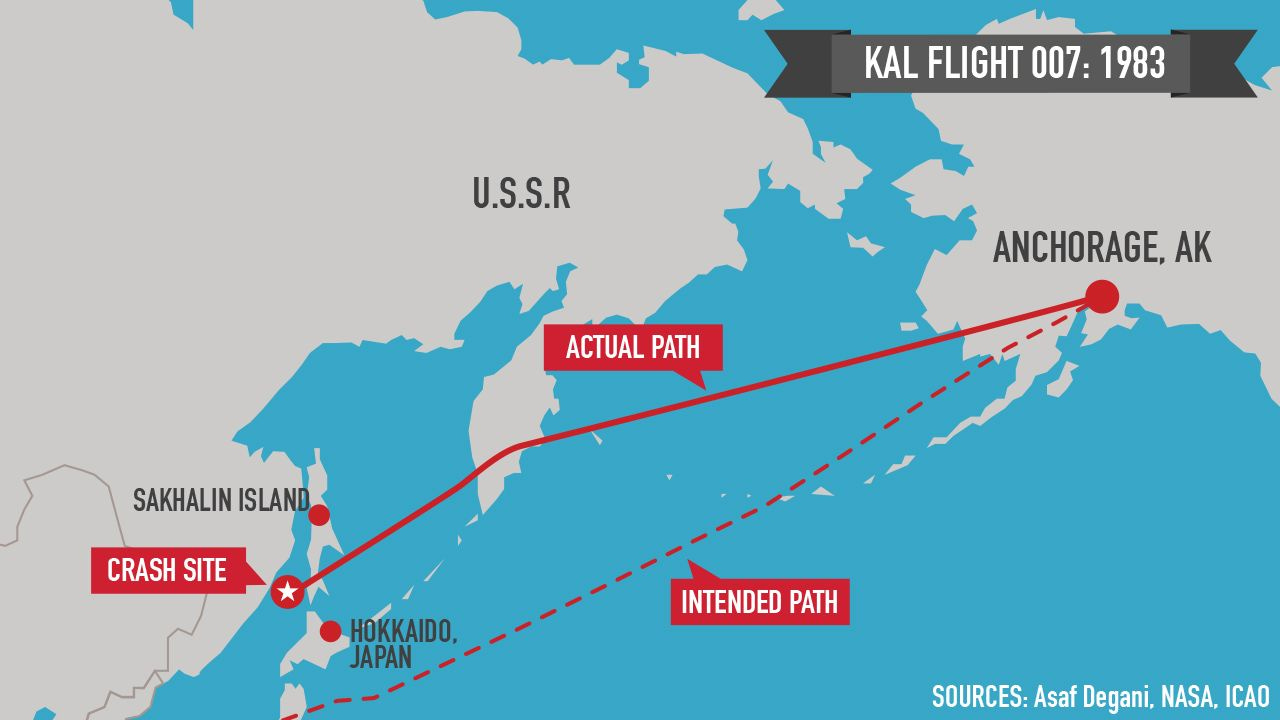
Let's explore a real-world application of the Kalman filter that significantly impacted the field of geolocation and global navigation systems. In the early 1980s, during the Cold War era, an incident involving a Korean Air Lines flight highlighted the critical importance of accurate geolocation and the need for reliable tracking systems.
The tragic event occurred in 1983 when Korean Air Flight 007, carrying 269 passengers and crew, veered off course into Soviet airspace and was shot down by a Soviet interceptor. The aircraft's deviation from its intended route was attributed to navigational errors, raising concerns about the vulnerability of global navigation systems and the potential for disastrous consequences.
In response to this incident, then-U.S. President Ronald Reagan took a significant step to enhance the accuracy and availability of geolocation technology. Recognizing the potential dangers associated with inaccuracies in navigation systems, Reagan issued a directive to make the Global Positioning System (GPS) accessible for civilian use.
(Patterson, 2013)
By opening up GPS technology to the public, Reagan aimed to prevent similar tragedies and promote the widespread adoption of precise geolocation tools. The decision to make GPS available for civilian applications marked a pivotal moment, shaping the landscape of navigation and contributing to the development of advanced tracking systems that are integral to various industries today.
In recent years, the Kalman filter, and Extended Kalman filter has played a crucial role in this context, as it becomes an essential component in the processing of airplane navigation data (Ehrman and Lanterman, 2008; Pullen et al., 2009; Alcalay et al., 2018; Bhattacharyya and Mute, 2020). By effectively handling the uncertainties and inaccuracies associated with satellite signals and sensor measurements, the Kalman filter improved the reliability of geolocation systems. Its ability to fuse information from multiple sources, such as GPS satellites and inertial sensors, allowed for more accurate and consistent location estimates.
In essence, the tragic incident involving Korean Air Flight 007 underscored the vital importance of robust geolocation systems and paved the way for advancements that have shaped the modern era of navigation. The Kalman filter, with its adeptness at handling uncertainties and optimizing data fusion, stands as a testament to the resilience of technology in the face of challenges, contributing to the safety and precision of geolocation applications worldwide.
References:
Bhattacharyya S, Mute D. Kalman Filter-Based RAIM for Reliable Aircraft Positioning with GPS and NavIC Constellations. Sensors (Basel). 2020 Nov 18;20(22):6606. doi: 10.3390/s20226606. PMID: 33218107; PMCID: PMC7698837.
G. Alcalay, C. Seren, G. Hardier, M. Delporte, P. Goupil,
An adaptive Extended Kalman Filter for monitoring and estimating key aircraft flight parameters,
IFAC-PapersOnLine,
Volume 51, Issue 24, 2018, Pages 620-627,ISSN 2405-8963, https://doi.org/10.1016/j.ifacol.2018.09.640.
(https://www.sciencedirect.com/science/article/pii/S2405896318323528)
Kalman, R. E. (1960). A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME--Journal of Basic Engineering, 82(Series D), 35-45.
M. Bertozzi, A. Broggi, A. Fascioli, A. Tibaldi, R. Chapuis and F. Chausse, "Pedestrian localization and tracking system with Kalman filtering," IEEE Intelligent Vehicles Symposium, 2004, Parma, Italy, 2004, pp. 584-589, doi: 10.1109/IVS.2004.1336449.
Pullen, Sam, and Jason Rife. "GNSS Applications and Methods, chapter 4: Fundamentals of GNSS III: Differential GNSS." Artech House (2009): 87-120.
Solving the UAV Localization Problem Using a Smooth Variable Structure FilteringSolving the UAV Localization Problem Using a Smooth Variable Structure Filtering - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/Extended-Kalman-Filter-Algorithm_fig5_300067587 [accessed 12 Feb, 2024]
US Govt GPS Applications. [(accessed on 5 November 2020)]; Available online: http://www.gps.gov/applications
Scherr, C., Lommatsch, G., Hooson, S., & Kaiser, T. (Year, Month Day). Underwater Navigation System. AUVSI Sub Support Team. Retrieved from https://ece.montana.edu/seniordesign/archive/SP14/UnderwaterNavigation/kalman_filter.html
Patterson, T. (2013, August 31). The downing of Flight 007: 30 years later, a Cold War tragedy still seems surreal. CNN. Retrieved from https://www.cnn.com/2013/08/30/world/asia/korean-air-flight-007-fast-facts/index.html
Trainer, J. How NASA Used the Kalman Filter in the Apollo Program. Jack Trainer: My Personal Blog. Retrieved from https://www.lancaster.ac.uk/stor-i-student-sites/jack-trainer/how-nasa-used-the-kalman-filter-in-the-apollo-program/
About the Author
Daniel Rusinek is an expert in LiDAR, geospatial, GPS, and GIS technologies, specializing in driving actionable insights for businesses. With a Master's degree in Geophysics obtained in 2020, Daniel has a proven track record of creating data products for Google and Class I rails, optimizing operations, and driving innovation. He has also contributed to projects with the Earth Science Division of NASA's Goddard Space Flight Center. Passionate about advancing geospatial technology, Daniel actively engages in research to push the boundaries of LiDAR, GPS, and GIS applications.