Unfolding Earth's Secrets: The Evolution of Geodesy from Antiquity to Today's Digital Frontiers
Welcome to TechTerrian where we explore all things LiDAR, GIS, and geospatial tech.
Now as interesting and flashy as LiDAR seems, it’s a limited tool by itself; the true power of LiDAR comes when you geolocate it to a true position on the Earth. Today continuing our series on geolocation, we will take a deep background dive into geodesy. Geodesy is a very old field of science that aims to accurately measure the Earth.
Now you may be thinking, that measuring the Earth doesn’t need its own field, but as we will discover in this article, it’s a highly technical field with far-reaching impact. Let’s start with some history.
Geodesy in the Ancient World
We begin our journey in the 3rd century BC. A man by the name of Eratosthenes was contemplating the curved nature of the Earth’s surface. Eratosthenes was a scholar, mathematician, and chief librarian at the Library of Alexandria, and he had heard a report that in the city of Syene (now Aswan, Egypt), vertical objects such as columns or obelisks cast no shadows at noon on the summer solstice. Intrigued by this, he wondered if the same was true in his hometown of Alexandria (Dutka, 1993).
On the summer solstice, Eratosthenes observed that in Alexandria, vertical objects did cast shadows at noon, but at an angle. Now this made no sense on a flat earth, but was perfectly reasonable on a curved surface. Therefore, Erathosthenes concluded that the Earths surface must be curved and went about calculating its circumference.
Eratosthenes then hired someone to measure the distance between Alexandria and Syene. The measurement, obtained by pacing the distance, was around 800 kilometers (500 miles). Knowing the distance and the angle of the shadow, Eratosthenes used geometry to calculate the Earth's circumference. He treated the Earth as a sphere and used the angle of the shadow as the central angle of a circle, with the distance between Syene and Alexandria as the arc length. This allowed him to estimate the Earth's circumference surprisingly accurately (Dutka, 1993). The result was remarkably close to modern measurements, showcasing Eratosthenes' brilliance in using simple observations and mathematical principles to deduce fundamental properties of our planet.
Illustration of Eratosthenes' method for calculating the Earth's circumference, demonstrating the use of shadow measurements and geometric principles to estimate the size of the planet. Adapted from "The History of Geodesy" by the National Oceanic and Atmospheric Administration (NOAA), National Ocean Service, 2024 (https://oceanservice.noaa.gov/education/tutorial_geodesy/geo02_hist.html).
Greeks in India:
The story continues with the interaction between Greek and Indian civilizations, following Alexander the Great's incursion into the Indian subcontinent in the 4th century BCE and the subsequent founding of the Northern India-Greek Kingdom. His conquests and establishment of Greek Kingdoms in Bactria (Afghanistan) and northern India led to a rich cross-pollination of ideas in various fields, including geodesy, astronomy, and mathematics. This period of cultural exchange contributed significantly to the development of scientific thought in both regions.
(Encyclopedia Britannica, 2024)
https://www.worldhistory.org/Indo-Greek/
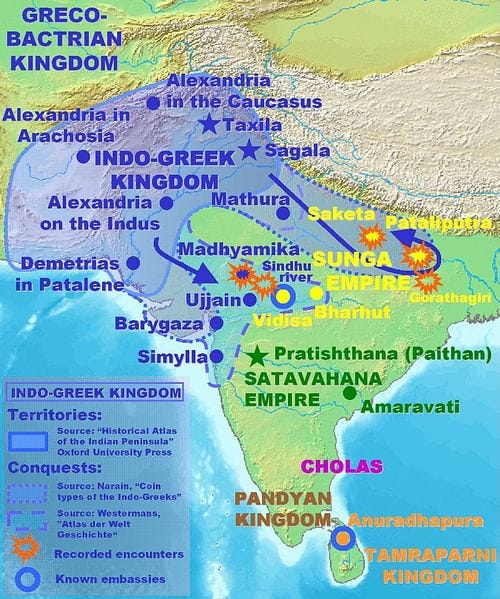
These maps delineates the expansive reach of Alexander the Great's empire at its zenith, stretching from Greece to the fringes of India, and highlights the often-overlooked Hellenistic realms of Bactria (Afghanistan) and the Greco-Indian Kingdom. These regions, where cultures converged and flourished, served as vibrant crossroads of Greek and Indian civilizations. Following Alexander's campaigns, these territories witnessed an unprecedented fusion of ideas, seeding advancements in science, art, and philosophy (Simonin, 2011; Wickramasinghe, 2021). The Bactrian and Greco-Indian kingdoms, marked here, stand testament to the enduring legacy of cultural exchange, embodying a unique blend of Greek and Indian influences that shaped the course of history long beyond Alexander's era. This map not only traces the physical boundaries of an empire but also sketches the contours of an intellectual and cultural mingling that enriched humanity's collective heritage.
Indian Contributions to Geodesy and Astronomy:
Pre-Greek Contributions
Long before the Greeks entered the Indian subcontinent, India had a thriving tradition of mathematics and astronomy. The Vedic texts, composed around 1500-500 BCE, contain early references to cosmology and the cycles of the sun and moon, indicating a keen interest in celestial phenomena (Iyengar, 2016). The Sulbasutras, texts on geometry associated with Vedic rituals, date from the 8th to 6th centuries BCE and demonstrate sophisticated knowledge of geometric principles, including the Pythagorean theorem, well before it was known in Greece (Agarwal, 2020).
Indian Scientific Developments
Indian scholars made significant strides in developing a system of numbers, including the concept of zero, which is one of India's greatest contributions to mathematics (Kaplan, 2000). Furthermore, the use of a decimal system and place-value notation facilitated calculations with large numbers, laying the groundwork for advances in algebra and arithmetic that were unparalleled in their time.
Astronomically, Indian scholars had developed elaborate theories on the motion of celestial bodies, planetary systems, and eclipses. Their observational techniques and calculations regarding the calendar and astronomical phenomena were highly sophisticated and formed the basis of later Indian astronomical works such as the Siddhantas (Hariprasad, 2018).
Symbol of Greek/Indian Cultural Exchange
https://www.worldhistory.org/image/340/buddha-with-hercules-protector/
This artistic representation of the Buddha shielded by Heracles (Hercules) not only epitomizes the cultural and philosophical synthesis between Greek and Indian traditions but also metaphorically reflects the intermingling of scientific and geodetic knowledge that these civilizations contributed to (Zheng, 2023). Just as Heracles' protective stance symbolizes the fusion of artistic motifs, it also mirrors the amalgamation of Greek and Indian scientific insights, particularly in the realms of astronomy, mathematics, and geodesy. The Greeks brought with them the geometric rigor and astronomical models developed by scholars like Euclid and Ptolemy, while India offered a rich tradition of mathematical innovation, including the concept of zero, place-value system, and early trigonometric ideas. This cross-cultural exchange facilitated advancements in geodesy. Indian contributions to astronomy, such as the detailed lunar and solar observations, were complemented by Greek geometric methods, enhancing the accuracy of geodetic measurements and mapping. The fusion of these scientific traditions helped lay the groundwork for more sophisticated understandings of the Earth's shape and size, as well as the development of navigation techniques that would later guide explorers and mapmakers.
Thus, the depiction of the Buddha under Heracles' guardianship serves as a powerful allegory for the shared legacy of Greek and Indian civilizations in enriching the scientific understanding of our world. It underscores how the blending of diverse cultural perspectives can lead to profound advancements in our quest to comprehend the natural world, illustrating that the roots of modern science are deeply entwined with the exchange of knowledge across civilizations.
Hellenistic Influence on Indian Science
Astronomy and Mathematics:
After Alexander's campaigns, the Seleucid Empire and later the Greco-Bactrian and Indo-Greek kingdoms maintained cultural and scientific exchanges between the Greek and Indian worlds. This interaction facilitated the transmission of Hellenistic astronomical and mathematical knowledge to India. Indian scholars had access to Greek works, and there was likely an exchange of ideas concerning the Earth's size, shape, and the calculation of celestial phenomena. One notable figure in this exchange was the Greek ambassador Megasthenes, who lived in the Mauryan court of Chandragupta Maurya. His detailed accounts of India, although lost to history and only known through later writers, likely included observations on Indian science and geography.
Influence on Indian Astronomy
The Greeks introduced the concept of the epicycle and deferent to Indian astronomy, which was used to explain the motion of planets. This Hellenistic model was adapted and used by Indian astronomers in the development of their own astronomical systems. The first few centuries CE saw the emergence of the Siddhantic era of Indian astronomy, which showed significant Greek influences in its theoretical foundations.
Aryabhata and Later Scholars
Indian mathematicians and astronomers like Aryabhata, who came centuries after the Greek invasion, may have been influenced by Hellenistic scientific thought, either directly through remaining Greek communities in India or through the assimilation of Greek astronomical ideas into Indian scholarly traditions.
Transmission Back to the West
The synthesis of Greek and Indian scientific ideas not only enriched Indian astronomy and mathematics, but also contributed to the body of knowledge that would eventually flow back to the Arab world and into Europe during the Middle Ages. The translations of Indian texts into Arabic in the early medieval period included works that had integrated Hellenistic and Indian scientific ideas, thus influencing the Islamic Golden Age and, later, the Renaissance in Europe.
Legacy
The legacy of the Greek presence in India, particularly in the realm of scientific thought, is a testament to the power of cultural exchange in advancing human knowledge. The interaction between Greek and Indian scholars contributed to significant advancements in geodesy, astronomy, and mathematics, illustrating how the fusion of ideas from different civilizations can lead to profound developments in scientific understanding.
Astronomy and Mathematics in the Medieval Sassanid Persian Empire:
The Sassanid period is noted for its significant contributions to astronomy, which is closely linked to geodesy. The Sassanids maintained and expanded upon the astronomical knowledge inherited from the Babylonians, Greeks, and Indians. They established observatories and promoted the study of celestial phenomena, contributing to more accurate calendars and timekeeping, which are essential for geodetic measurements.
One of the most famous Sassanid astronomers, mathematicians, and astrologers was Zaradusht al-Balkhi, who is known to have made significant contributions to the Zij al-Sindhind, an astronomical table based on Indian and Hellenistic elements, further developed during the Islamic Golden Age (Pingree, D., 1989). Such tables included information on the positions of stars, the movement of the planets, and the calculation of eclipses, which are vital for navigation and determining geographical coordinates.
https://www.iranchamber.com/history/sassanids/sassanids.php
A Sphere or Something More?
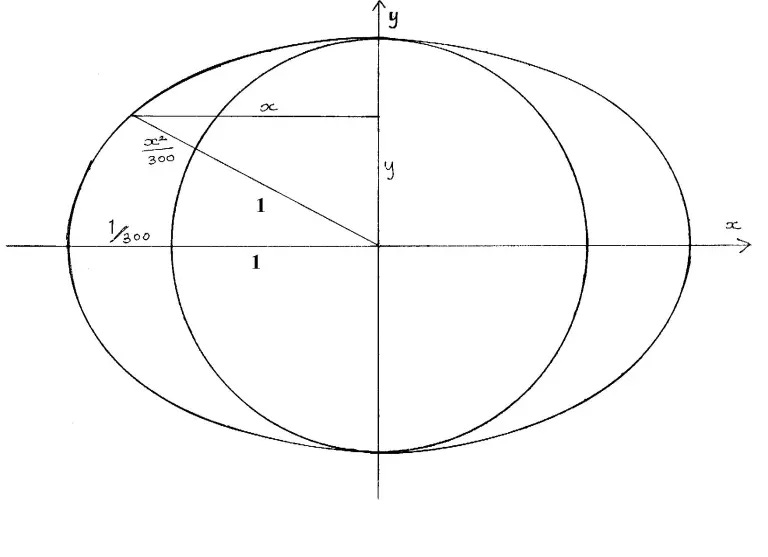
As geodesy advanced, scientists grappled with the Earth's exact form. It wasn't merely a perfect sphere, but rather an oblate spheroid. Moreover, Earth, far from being a perfectly smooth spheroid, exhibits gravitational lumps and bumps across its surface. These irregularities, caused by variations in mass distribution, create a fascinating mosaic of elevations and depressions. Mountains, valleys, and subterranean structures contribute to these deviations, each exerting its own gravitational influence (Danson, 2009). At the equator, where centrifugal forces generated by Earth's rotation counteract gravity, a perceptible bulge occurs. The Earth's equatorial belt becomes a dynamic region, marked by a subtle but noticeable departure from a perfect sphere; instead, it’s more of a tomato shape.
The Scottish Schiehallion Experiment: Unraveling Earth's Gravitational Secrets
https://squishtheory.wordpress.com/the-earths-equatorial-bulge/
In the hushed landscapes of 18th-century Scotland, against the backdrop of the majestic Schiehallion mountain, an experiment unfolded that would unveil the intricate relationship between mass distribution and Earth's gravitational forces. In 1774, astronomers Charles Mason and Charles Dixon embarked on a pioneering quest to measure the gravitational attraction of this imposing mountain. Little did they know that their endeavors would contribute crucial insights to our understanding of Earth's complex shape (Danson, 2009)
The Experiment Unveiled:
Mason and Dixon's objective was clear: measure the gravitational pull of Schiehallion and use this data to determine the Earth's average density. They placed a set of plumb lines at various locations around the mountain, carefully observing the deflection caused by the mountain's gravitational pull. By triangulating these measurements, they aimed to deduce the mass of Schiehallion and, by extension, the influence of mass distribution on gravity.
Gravitational Variations:
The deflections observed during the Schiehallion Experiment weren't uniform, showcasing the localized influence of the mountain's mass on gravity. This non-uniform gravitational field hinted at the irregularities beneath the Earth's surface—mountains, valleys, and subterranean structures—that contribute to the planet's unique gravitational landscape.
Drawing the Conclusion:
While Mason and Dixon's experiment did not directly confirm Earth's oblate spheroid shape, it added a pivotal piece to the puzzle. The variations in gravitational pull around Schiehallion highlighted the nuanced relationship between mass distribution and gravity, emphasizing that Earth is far from a homogeneous, perfect sphere.
Earth's Unique Character:
In the tapestry of Earth's gravitational field, the Schiehallion Experiment revealed the first strokes of irregularities—lumps and bumps that contribute to our planet's distinctive character. The experiment, though conducted on a single mountain, alluded to the broader truth: Earth's gravitational landscape is a complex system, shaped by its geological features and the distribution of mass beneath its surface
Following the intellectual legacy left by Eratosthenes and others, the quest for geodetic understanding in the early 18th century took an intriguing turn with the initiation of the Longitude Prize. Eratosthenes, centuries earlier, had brilliantly calculated the Earth's circumference using the angles of the sun's rays at different locations. Now, as sailors faced the pressing need to determine longitude at sea, the Longitude Prize became the inaugural milestone in a renewed journey of geodesy (Sobel, 1995)
The Longitude Prize:
Understanding longitude was of paramount importance, especially during the Age of Exploration, due to its direct impact on maritime navigation. The ability to determine a ship's longitude at sea was crucial for accurate and safe voyages across the vast oceans. Before reliable longitude measurements, sailors often faced the risk of getting lost, miscalculating routes, and encountering navigational perils. The Longitude Prize, initiated by the British Admiralty in the 18th century, reflected the urgent need for a solution. Knowing longitude enabled sailors to establish their east-west position, helping them plot more precise courses, avoid hazards, and reach their destinations efficiently (Sobel, 1995). The advancements in timekeeping technology, particularly exemplified by John Harrison's marine chronometer, not only transformed navigation but also laid the foundation for broader geodetic principles. The knowledge of longitude not only safeguarded lives and valuable cargo but also ushered in a new era of maritime exploration, trade, and scientific understanding of Earth's spatial dimensions.
The Longitude Prize and the subsequent developments, especially John Harrison's marine chronometer, marked a pivotal point in geodetic exploration (Sobel, 1995). The accurate measurement of time at sea, a solution driven by the Longitude Prize competition, became intricately linked with geodesy. Harrison's chronometer, allowing sailors to precisely determine their position by comparing local time with a reference location, showcased the profound connection between timekeeping and the Earth's spatial dimensions.
In the geodetic context, the Longitude Prize demonstrated that advancements in understanding the Earth's shape were not solely confined to continental measurements, but extended to the vast expanses of the ocean. The necessity of solving the longitude problem underscored the practical applications of geodesy, emphasizing its relevance in addressing real-world challenges faced by mariners navigating the globe.
The journey from Eratosthenes' calculations to the Longitude Prize marked an evolution in the application of geodesy—from understanding the Earth's size to addressing the intricacies of navigation. As we delve into the subsequent experiments and surveys, we witness a continuous thread weaving through the fabric of geodetic history. Each chapter builds upon the other, contributing to our evolving comprehension of the Earth's dynamic and ever-fascinating characteristics.
In the late 18th century, amidst the intellectual fervor of the Enlightenment, two French astronomers, Jean-Baptiste Delambre and Pierre Méchain, were tasked by the French Academy of Sciences to measure a tiny, but crucial unit known as an arcsecond (Williams, 2014).
The arcsecond, a unit of angular measurement, is incredibly small—equal to 1/3600th of a degree. Delambre and Méchain recognized that by precisely measuring the length of a meridian arc, they could glean insights into the Earth's overall dimensions. This task would require meticulous surveying and took six years to complete, involving detainment by revolutionaries during the French Revolution, accusations of espionage, financial challenges, and political suspicion (Williams, 2014).
Close-Up of Original Paper on Triangulation:
Here we see a close-up view of the original paper illustrating the technique of triangulation. This image provides a detailed look at the geometric principles and calculations involved in the measurement process.
Map of France with Triangulation Traversal:
Map showcasing the extensive use of triangulation in measuring distances across France. The triangulation points are depicted, illustrating the meticulous process astronomers Delambre and Méchain undertook to traverse the entire country and measure the Earth's dimensions in the late 18th century.
From 1792 to 1798, the duo undertook an expedition to measure the meridian from Dunkirk in the north to Barcelona in the south. Battling adverse weather conditions, political unrest, and the unpredictable nature of 18th-century surveying instruments, Delambre and Méchain meticulously recorded their measurements (Williams, 2014).
Their approach was revolutionary. They employed a technique called triangulation, breaking down the vast distance into smaller, more manageable triangles. By carefully measuring the angles and distances within these triangles, they built a detailed and accurate picture of the meridian.
The results of their arduous efforts were staggering. Delambre and Méchain successfully determined the length of one degree of meridian arc, and subsequently, the Earth's equatorial radius. Their work laid the foundation for the development of the metric system and significantly contributed to our understanding of the Earth's shape.
However, the story doesn't end there. Méchain's measurements were later found to contain errors, leading to a small discrepancy in the final calculations. This discrepancy would be rectified by later generations of geodesists, but the saga of Delambre and Méchain remains a testament to the dedication and tenacity required in the pursuit of scientific knowledge. The arcsecond they measured might have been minuscule, but its impact on our understanding of the Earth was nothing short of monumental (Williams, 2014).
The measurements and calculations made by Jean-Baptiste Delambre and Pierre Méchain were foundational in the establishment of the metric system and, in particular, the definition of the meter.
Originally, the meter was defined as one ten-millionth of the distance from the North Pole to the Equator along the meridian passing through Paris. This definition was based on the results of their measurements, which aimed to determine the size and shape of the Earth. The idea was to create a standard unit of length that was universal and based on natural, reproducible phenomena.
In 1799, the French Academy of Sciences officially adopted the meter as a unit of length, making it part of the metric system. Over time, the definition of the meter has evolved, and today it is defined in terms of the speed of light in a vacuum.
Delambre and Méchain's work not only contributed to the establishment of the meter but also played a crucial role in advancing our understanding of geodesy and the Earth's shape, leaving a lasting impact on scientific measurement standards.
Navigating Earth's Mathematical Landscape: The Challenge of Lumps and Bumps
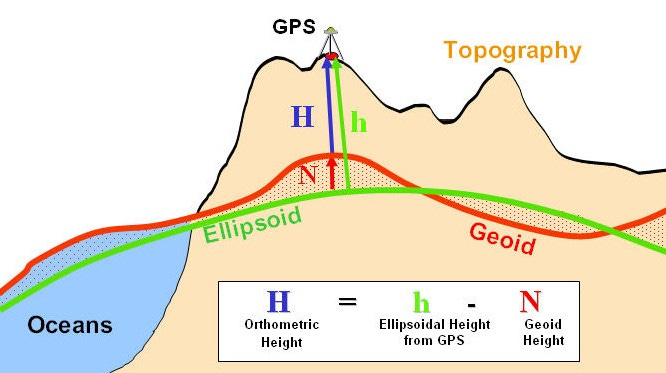
To better approximate the Earth, scientists use a model called the Geoid which represents the Earth as a surface of equipotential gravitational energy. It is an uneven sphere with bumps and undulations corresponding to changes in Earth’s gravitational field due to terrain, subterranean density differences, and mantle convection forces. Simply put, there is the same amount of gravitational potential energy at every point on the surface of the Geoid; if the planet’s oceans were perfectly calm, and could seep under continents they would align with the Geoid.
(UNAVCO, 2023)
The Geoid approximates mean sea level and serves as an important tool for depth measurements and GPS. For example, when a GPS reports your height above sea level, it is reporting your height above the Geoid, known as orthometric height. However, accurate mapping requires more precise mathematical operations, and the Geoid proves insufficient; other tools are required.
(UNAVCO, 2023)
Enter the Reference Ellipsoid:
Attempting to conduct mathematical calculations directly on the Earth's irregular surface is akin to navigating a landscape with unpredictable peaks and troughs. The sheer variety of elevations and gravitational anomalies introduces an inherent difficulty in performing accurate measurements and computations.
To circumvent the intricacies of Earth's surface, geodesists approximate it with a smooth mathematical shape known as a reference ellipsoid. This ellipsoid serves as a standardized, simplified model that captures the Earth's overall shape, allowing for more straightforward mathematical operations.
Not All Ellipsoids are Created Equal:
Here's where the plot thickens. While a single reference ellipsoid provides a useful generalization, Earth's irregularities vary across regions. Enter different reference ellipsoids tailored for specific parts of the globe. For instance, North America benefits from the GRS80 reference ellipsoid calculated to align with the continent's unique geodetic characteristics. Imagine the Earth's surface as a dynamic canvas, with each region painted by a distinct reference ellipsoid. GRS80 with its focus on North America, intricately captures the nuances of the continent's topography and gravitational field. In contrast, other ellipsoids may be better suited for different regions, providing the most accurate representation for localized calculations.
Navigating Earth's Terrain: The Crucial Role of Coordinate Systems
As we delve deeper into the realm of geodesy, we encounter a critical concept that bridges the gap between Earth's dynamic, three-dimensional surface and the two-dimensional realm of maps—the datum. In our quest to represent the round Earth on flat maps, datums become the linchpin, ensuring accuracy and coherence in cartographic endeavors. The Earth, with its undulating terrains and gravitational intricacies, is far from flat. Yet, when it comes to creating maps for navigation, exploration, and everyday use, we must confront the challenge of representing our spherical planet on a flat surface. This is where datums step into the spotlight.
The Datum Defined
A datum is essentially a reference framework—a mathematical model that aligns with the Earth's shape and provides a basis for mapping. It encompasses a specific ellipsoid (usually a reference ellipsoid) and a defined point on the Earth's surface, known as the origin or reference point. Together, these elements establish a standardized starting point for mapping a given area.
Reference Frame: A datum establishes a reference frame against which positions on the Earth's surface are measured. This frame typically includes a specific reference point or set of points, as well as an orientation and scale factor.
Reference Ellipsoid: A datum is often defined in relation to a reference ellipsoid. This ellipsoid serves as the geometric basis for the datum and provides a standardized approximation of the Earth's shape.
Origin: The datum specifies a reference point, often called the origin or datum point, from which all measurements are made. This point may be located on the Earth's surface or at its center, depending on the datum.
Orientation: The orientation of the coordinate axes is defined within the datum, establishing the directions of latitude, longitude, and often elevation.
Parameters: Datums may include additional parameters such as scale factors, translations, and rotations to account for variations in the Earth's shape and the alignment of the coordinate system with respect to the Earth's surface.
Regional or Global Coverage: Datums can be designed for specific regions, such as national or local coordinate systems, or they can be global in scope, intended for use across entire continents or the entire planet.
From Ellipsoid to Flat Map
Imagine the Earth's surface as a canvas draped over the chosen ellipsoid. The datum acts as the anchor, ensuring that when we project the spherical Earth onto a flat map, the representation is both accurate and consistent. Different regions employ different datums, each tailored to the local geodetic characteristics, minimizing distortions in measurements and promoting precision.
NAD83 and WGS84: Familiar Datums
Two widely used datums are the North American Datum of 1983 (NAD83) and the World Geodetic System of 1984 (WGS84). NAD83 caters specifically to North America, aligning its ellipsoid with the continent's unique features. WGS84, on the other hand, serves as a global datum, essential for satellite navigation systems like GPS.
The Art of Cartography: Ensuring Accuracy
In the cartographer's workshop, the chosen datum is the artisan's brushstroke. It determines how accurately the Earth's features are portrayed, influencing everything from distances and angles to the shape and orientation of mapped objects. The choice of datum ensures that the flat representation maintains fidelity to the true, spherical Earth.
Decoding Map Distortions: Mercator, Peters, and the Shadows of History
Unwrapping the Globe:
Imagine trying to peel an orange and flatten its skin onto a table. No matter how carefully you try, the peel will stretch, tear, and distort. Similarly, cartographers face a similar challenge when transforming the spherical Earth onto flat maps, leading to inevitable distortions.
https://mathworld.wolfram.com/CylindricalProjection.html
The Mercator Dilemma: Stretching the Truth
Enter the Mercator projection, a navigational favorite due to its ability to preserve angles and straight lines of bearing; However, this projection significantly distorts the sizes of continents (while preserving shapes), especially as you move towards the poles. Greenland appears disproportionately vast, setting the stage for historical misperceptions of countries' relative sizes.
The Peters Perspective: A Quest for Equity:
In response to the Mercator's size distortions, the Peters projection emerged as an alternative. Advocates argue that it provides a fairer representation of land masses, particularly those near the equator. However, even the Peters projection is not without its criticisms, highlighting the ongoing complexities in cartographic choices.
West Wing's Insight: Mapping and Imperialistic Narratives
The West Wing video on the Peters vs. Mercator projections masterfully underscores how map choices can influence perspectives. The Mercator's historical use, portraying European nations as more dominant, may have subtly fostered imperialistic attitudes. This historical context adds depth to the seemingly technical decisions made by cartographers.
Beyond Cartography: The Socio-Political Landscape
Map projections, seemingly innocuous, carry echoes of history and influence how we perceive the world. The socio-political implications of choosing one projection over another extend beyond geography, shaping narratives, and reinforcing certain perspectives. The shadows of history are cast on these maps, telling stories that extend far beyond the paper they're printed on.
In the realm of cartography, the challenge of representing the spherical Earth on a flat surface necessitates trade-offs between preserving the true shapes or the accurate sizes of continents. Projections like the Mercator retain the shape of continents, making them invaluable for navigation as they keep angles and directions intact but at the cost of distorting sizes, especially as one moves further from the equator. Conversely, projections such as the Gall-Peters prioritize maintaining the relative sizes of continents, offering a more equitable representation of developing countries often misrepresented in size by other projections. However, this size accuracy comes with a compromise on the shapes, which can appear elongated or distorted. This dichotomy underscores a fundamental cartographic principle: no single map projection can perfectly capture all aspects of the Earth's surface, leading to the development of various projections each tailored to specific needs, whether for educational purposes, navigational aids, or thematic mapping.
Navigating the Map's Shadows
As we navigate the complex terrain of map projections, it becomes clear that cartography is not a neutral endeavor. Every choice has consequences, and the shadows of historical decisions linger in the maps we use today. Understanding the socio-political nuances of map projections adds layers to our comprehension of the world, reminding us that the stories told on maps are not just lines and colors but reflections of complex histories and narrative
Universal Transverse Mercator:
Following the discussion on the Mercator projection and its notorious distortion of continent sizes, which magnifies areas closer to the poles while shrinking those near the equator, we introduce the Universal Transverse Mercator (UTM) system as an alternative. The UTM is a global map projection system that divides the world into a series of 6-degree longitudinal zones, each with its own central meridian.
This cylindrical map projection minimizes distortion within each zone by effectively segmenting the Earth’s surface into manageable pieces. Unlike the Mercator projection, which is best suited for navigation due to its angle-preserving properties, the UTM system excels in maintaining relative spatial accuracy and scale, making it highly beneficial for topographical mapping, land surveying, and construction projects. Each UTM zone uses a transverse Mercator projection, which significantly reduces the distortion of distance, area, and shape by confining the extent of the projection to smaller geographic areas. This makes the UTM an indispensable tool in precision-based applications where accurate geolocation and detailed spatial analysis are paramount.
The 3DEP Program: A Foundation for Advanced Geospatial Analysis
The U.S. Geological Survey's 3D Elevation Program (3DEP) is a groundbreaking effort that aims to systematically collect enhanced elevation data across the United States. Utilizing state-of-the-art LiDAR (Light Detection and Ranging) technology, 3DEP generates high-resolution topographic maps with an accuracy measured in arcseconds, first measured by Delambre and Méchain and since improved on, providing detailed three-dimensional representations of the Earth's surface.
Transforming Data into Actionable Insights
Flood Risk Management: One of the critical applications of 3DEP data is in flood risk assessment and management. The detailed elevation data helps hydrologists and planners identify flood-prone areas with greater precision, facilitating the development of more effective flood mitigation strategies and infrastructure designs.
Infrastructure Development: Urban planners and engineers rely on 3DEP data for infrastructure projects, from road and bridge construction to utility planning. The elevation data aids in optimizing routes, assessing potential environmental impacts, and ensuring structures are built in locations that minimize risk and maximize efficiency.
Environmental Conservation: Conservationists use 3DEP data to monitor and manage natural habitats, track erosion patterns, and plan for conservation efforts. The detailed topographic information supports biodiversity conservation by identifying critical habitats for endangered species and assessing changes in land use.
Agriculture and Resource Management: Farmers and resource managers leverage 3DEP data for precision agriculture, optimizing irrigation systems, and managing land resources more sustainably. The elevation data allows for the precise application of water, fertilizers, and pesticides, reducing waste and improving crop yields.
Emergency Response and Recovery: In the aftermath of natural disasters, 3DEP data is invaluable for damage assessment and recovery planning. Emergency responders can quickly identify affected areas, plan evacuation routes, and allocate resources more effectively, saving lives and reducing recovery times.
The Power of Public Data
A pivotal aspect of the 3DEP initiative is its commitment to making elevation data publicly available. This openness ensures that researchers, government agencies, businesses, and the public have access to high-quality geospatial data, democratizing the use of advanced mapping technologies and fostering innovation across various fields. By providing a shared resource, 3DEP enhances collaboration, drives scientific discovery, and supports informed decision-making at all levels of society.
Looking Forward: The Future of Surveying, 3DEP and Geospatial Science
As we look to the future, the 3DEP program stands as a model for geospatial data collection and utilization. The ongoing refinement of LiDAR technology and the expansion of the program's coverage promise even greater accuracy and detail in elevation modeling. Moreover, the integration of
The narrative arc of geodesy, from the ancient endeavors of Eratosthenes to the sophisticated digital landscapes shaped by the 3DEP program, underscores a profound journey of human curiosity, innovation, and the relentless pursuit of understanding our planet. Each chapter in this historical saga not only highlights the advancements in measuring the Earth but also showcases the indispensable role of accurate geolocation and cartography in realizing these achievements.
At its core, the essence of geodesy lies in its quest to pinpoint our position on the Earth with precision and to map the contours of our world with clarity. This quest has evolved dramatically over the millennia, propelled by the confluence of diverse cultures and the exchange of knowledge across civilizations. The fusion of Greek geometric rigor with Indian mathematical innovations, the meticulous observations of Islamic scholars, and the transformative impact of the Longitude Prize all reflect milestones in this ongoing journey. These pivotal moments in history were not merely about understanding the Earth's shape or size but about enhancing our ability to navigate, explore, and coexist with our environment.
The advent of the 3DEP program represents the latest frontier in this endeavor, harnessing the power of LiDAR and modern geospatial technologies to create a multidimensional canvas of the United States. This initiative, rooted in the principles of geodesy, transcends the mere collection of data; it embodies the synthesis of centuries-old dreams and the capabilities of contemporary science. By offering arcsecond resolution, 3DEP provides an unprecedented level of detail, transforming raw data into actionable insights for flood management, infrastructure development, environmental conservation, and beyond.
This progression from ancient calculations to digital elevation models illustrates a fundamental truth: our advancements in geodesy, cartography, and geospatial science are deeply reliant on precise geolocation. The ability to accurately determine our position on the Earth is the cornerstone upon which the edifice of modern mapping and analysis is built. Without the accurate knowledge of where things are—or where one is located—our efforts in navigating, surveying and conservation would be impossible.
As we continue to push the boundaries of what is possible with geospatial technology, we do so standing on the shoulders of giants. The historical narrative of geodesy is not just a record of past achievements; it is a guiding path forward. It reminds us that our quest to measure and map the Earth is a testament to our shared heritage of exploration and discovery on this planet that we all share. In the intricate tapestry of our planet's geography, each point of data, each line on a map, is a verse in an ongoing story—a story that connects us across time and space, from the ancient world to the digital age.
That concludes our discussion on the history, mathematical basics, and applications of geodesy. There is so much more I could go into, so if you like this type of content and would like to see more please leave a comment below.
Thank you for reading; I really appreciate it!
I hope you’ve learned something and please like, subscribe, and share; it helps me out immensely.
References:
Agarwal, R. P., 2020. Pythagorean theorem before and after Pythagoras. Advanced Studies in Contemporary Mathematics, 30(3), pp. 357-389.
"Alexander the Great." Encyclopedia Britannica. Accessed on February 17, 2024. URL: https://www.britannica.com/biography/Alexander-the-Great.
Danson, E., 2009. Weighing the World: The Quest to Measure the Earth. 1st ed. Oxford University Press.
Dutka, J., 1993. Eratosthenes’ Measurement of the Earth Reconsidered. Arch. Hist. Exact Sci. 46, 55–66. Available at: http://www.jstor.org/stable/41134135.
Hariprasad, P. P. S., 2018. How ancient are Vedas, Vedanga Jyotisha and Surya Siddhanta? CrossAsia-Repository.
Kaplan, R., 2000. The Nothing That Is: A Natural History of Zero. Oxford University Press, USA.
Pingree, D., 1989. Classical and Byzantine Astrology in Sassanian Persia. Dumbarton Oaks Pap. 43, 227-239.
Simonin, A. (2011, April 28). "Indo-Greek." World History Encyclopedia. Retrieved February 17, 2024, from https://www.worldhistory.org/Indo-Greek/.
Sobel, D., 1995. Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time. Walker and Company, USA.
Sobel, D., 1995. Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time. Walker and Company, New York.
UNAVCO. (2023). Geoid Height Calculator. EarthScope Consortium, National Science Foundation’s Geodetic Facility for the Advancement of Geoscience (GAGE). Retrieved from https://www.unavco.org/software/geodetic-utilities/geoid-height-calculator/geoid-height-calculator.html
Wickramasinghe, C. S. M., 2021. The Indian Invasion of Alexander and the Emergence of Hybrid Cultures. Indian Historical Review, 48(1), pp. 69-91. Available at: https://doi.org/10.1177/03769836211009651.
Williams, J. H., 2014. Measurement in the Modern World. In: Defining and Measuring Nature: The Make of All Things. Morgan & Claypool Publishers.
Zheng, Y., 2023. A Study of the History of the Development of Buddhist Iconography. J. Educ. Humanit. Soc. Sci. 11, 119-124.
About the Author
Daniel Rusinek is an expert in LiDAR, geospatial, GPS, and GIS technologies, specializing in driving actionable insights for businesses. With a Master's degree in Geophysics obtained in 2020, Daniel has a proven track record of creating data products for Google and Class I rails, optimizing operations, and driving innovation. He has also contributed to projects with the Earth Science Division of NASA's Goddard Space Flight Center. Passionate about advancing geospatial technology, Daniel actively engages in research to push the boundaries of LiDAR, GPS, and GIS applications.