Can a Transformer Represent a Kalman Filter?: a Review
Attention Transformer Application in Control Theory
In this issue of TechTerrain, we continue our dive into the intersection of artificial intelligence and control theory, exploring the application of Transformer architectures in linear dynamical systems. Our discussion will cover:
Kalman Filter Overview: A brief review of the Kalman Filter's role in state estimation and control.
Transformers as Alternatives: Investigating the feasibility of Transformers for tasks traditionally handled by the Kalman Filter.
Extension to Control Systems: Assessing the potential of Transformers within the Linear-Quadratic-Gaussian (LQG) model.
Theoretical and Practical Implications: Analyzing the theoretical foundations and practical applications of employing Transformers in this domain.
Study Motivations and Insights: Highlighting the driving forces behind this exploration and its implications for deep learning and control theory. We took a detailed dive into the Kalman filter in a previous article, I highly recommend a read!
For a deeper dive into the mathematics behind Kalman Filters I highly suggest this read!
Also see this post for further discussion:
Introduction
The journal article titled "Can a Transformer Represent a Kalman Filter?" delves into the application of Transformer architectures to fundamental challenges in state estimation and control.
The paper opens with a focus on the problem of filtering in linear dynamical systems, where the task is to estimate the state of a system given noisy observations. Traditionally dominated by the Kalman Filter, the authors pose the question: Can Transformers, known for their prowess in natural language processing, offer a viable alternative in this domain? As we unravel the intricacies of their exploration, we witness a deep dive into the theoretical foundations and the practical implications of employing Transformers for state estimation.
Moving beyond filtering, the study extends its gaze to the realm of control in linear systems. Here, the authors set out to investigate whether a Transformer-based approach can seamlessly step into the shoes of the Kalman Filter in the Linear-Quadratic-Control (LQG) model. The goal is ambitious yet compelling: to regulate the system's state using Transformer-induced control policies. But can these complex neural architectures effectively replace classical control methods?
In this review, we will navigate through the key findings, theorems, and insights presented by the authors. From the motivations driving this exploration to the mathematical rigor underpinning their methodology, we'll dissect the paper's contributions and its potential implications for both the fields of deep learning and control theory.
Kalman Filter Review
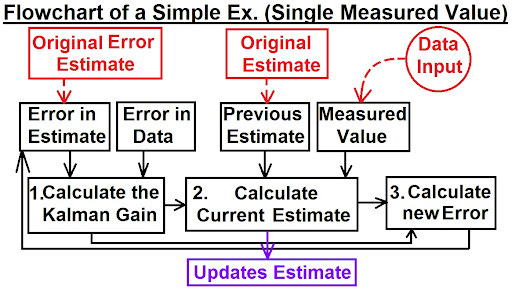
In the realm of data and control systems, the Kalman Filter emerges as a sophisticated tool, akin to a high-tech compass steering through the complexities of noisy information. Imagine it as a refined algorithmic conductor, orchestrating a symphony of data to pinpoint the most accurate state estimation.
At its core, the Kalman Filter excels in scenarios where measurements are imprecise, and disturbances abound (Kalman, 1960). Take, for instance, the guidance systems of spacecraft, autonomous vehicles, or even tracking the position of an underwater robot. In these applications, the Kalman Filter plays the role of an intelligent decision-maker, continuously refining its understanding of the system's state based on new measurements taken in time.
Here's how it works:
1. Prediction Phase: Looking Forward
The Kalman Filter starts by predicting the current state based on the previous state and the system dynamics. It forecasts where things should be without considering measurements.
2. Update Phase: Blending Measurements and Predictions
It then receives real-world measurements, often imperfect and laden with noise. The filter intelligently weighs these measurements against its predictions, considering their reliability. Precise measurements get more influence, while less reliable ones have less impact.
http://www.ilectureonline.com/lectures/subject/SPECIAL%20TOPICS/26/190
3. Optimal Fusion: Minimizing Uncertainty
What makes the Kalman Filter powerful is its ability to optimize the fusion of prediction and measurement. It doesn't just accept data blindly; it calculates the optimal blend, minimizing the overall uncertainty in the process.
4. Iterative Refinement: A Continuous Cycle
The process repeats as new measurements come in. The filter continuously refines its estimation, dynamically adjusting to changes in the system and the quality of incoming data.
This coordination between prediction and measurement, with a touch of mathematical elegance, makes the Kalman Filter a standard tool in applications where precision and adaptability are paramount. It's like a data maestro orchestrating harmony from the cacophony of uncertainties, ensuring that the system navigates smoothly through the intricate seas of information.
Study Motivations:
The study is motivated by exploring the possible application of Transformer architectures, a type of deep learning model, to the problems of state estimation and control in linear dynamical systems. The study specifically focuses on two main problems:
Filtering in Linear Dynamical Systems:
The study investigates the use of Transformers for filtering in partially observed linear systems. Filtering involves estimating the state of a system based on noisy observations. The Kalman Filter is a well-known algorithm for this purpose, and the study explores whether a Transformer-based approach can provide a reasonable approximation to the Kalman Filter.
Measurement-Feedback Control in Linear Dynamical Systems:
The study extends its exploration to the problem of control in linear systems, where the goal is to regulate the state of the system using observations. In particular, the study considers the Linear-Quadratic-Control (LQG) model and aims to investigate if a Transformer-based approach can be used in place of the Kalman Filter in the LQG controller.
Computational Efficiency: Transformers have gained popularity in various natural language processing tasks due to their parallelizable and scalable nature. The study explores whether these advantages can be leveraged in the context of state estimation and control in linear systems.
Adaptability to Nonlinearities: Linear dynamical systems are common models, but many real-world systems exhibit nonlinear behavior. The study explores whether Transformer-based methods can offer better adaptability to nonlinearities without the need for explicit linearization of the model.
Exploring Alternatives to Classical Methods: While classical methods like the Kalman Filter are well-established and widely used, exploring alternatives can be beneficial, especially in scenarios where traditional methods face challenges or are computationally expensive.
In summary, the motivation is to investigate the feasibility of using Transformer architectures in the context of state estimation and control for linear dynamical systems, with a focus on their potential advantages in terms of computational efficiency and adaptability to nonlinearities. The study aims to provide insights into the capabilities and limitations of Transformer-based approaches in comparison to traditional methods.
Introduction:
The introduction of the article sets the stage by highlighting the widespread success of transformers in various domains, such as computer vision, natural language processing, and robotics. However, the lack of a formal theory explaining their capabilities motivates the study presented in the paper. The primary focus is on investigating whether transformers, specifically, can be utilized for Kalman Filtering in linear dynamical systems.
The authors pose fundamental questions regarding the compatibility of the nonlinear structure of transformers with Kalman Filtering. They inquire about the representation of the Kalman Filter within a transformer, considering factors such as the necessity of positional encoding and the required size of the transformer.
The key contributions of the paper are outlined, introducing the concept of the "Transformer Filter." The construction of this transformer involves a two-step reduction. First, it is demonstrated that a self-attention block can accurately represent a Gaussian kernel smoothing estimator. This kernel has a system-theoretic interpretation related to the closeness of state estimates. The second step involves showing that this kernel smoothing algorithm approximates the Kalman Filter, with a controllable level of accuracy through a temperature parameter.
Additionally, the article explores how the Transformer Filter can be integrated into a measurement-feedback control system. The closed-loop dynamics induced by the Transformer Filter are discussed, addressing the challenges posed by the nonlinearity of the state estimates. The paper claims that the Transformer Filter can closely approximate an LQG controller, providing a sense of weak stabilization and driving the state into a small ball centered at zero. The results are suggested to hold even when considering H∞ filter or H∞ controller as reference algorithms.
Overall, the introduction provides a clear overview of the motivation, questions addressed, and the key contributions of the paper, setting the stage for the detailed exploration of transformers in the context of Kalman Filtering and control systems.
Preliminaries Section:
In this section, the article delves into the preliminaries, setting up the foundational concepts for the subsequent discussion. Let's break down the key points:
Filtering and Control in Linear Dynamical Systems:
The authors begin by introducing the problem of Filtering in Linear Dynamical Systems, specifically a partially observed linear system. The Kalman Filter is highlighted as a well-known algorithm in this context, providing optimal mean-square estimates when disturbances are stochastic. The recursive form of the Kalman Filter and its equivalence with the H∞ filter is mentioned.
The second problem addressed is Measurement-Feedback Control in Linear Dynamical Systems, where a control input is introduced. The Linear-Quadratic-Control (LQG) model is discussed, emphasizing the use of the Kalman Filter in generating state estimates for optimal control. The optimal policy using the Kalman Filter estimate and its adjustment for control input are presented.
Assumptions and Facts:
Assumptions are made regarding the observability of (A, C) and controllability of (A, B). Two facts are stated: Fact 1, establishing the existence of matrices for stable A, and Fact 2, stating stability conditions for linear measurement-feedback controllers.
In the context of control theory, especially when discussing the Linear Quadratic Regulator (LQR), Linear-Quadratic-Gaussian (LQG) controller, or Kalman Filter, the terms "observability" and "controllability" are crucial. The matrices A, B, and C represent different aspects of the system's model:
- A is the state matrix, representing the system's dynamics.
- B is the input matrix, representing how control inputs affect the system's state.
- C is the output matrix, representing how the system's state is observed or measured.
Observability (A, C):
Observability concerns the system's ability to infer the complete internal state of the system from its outputs over time. A system is considered observable if, for any possible sequence of state and control vectors, the current state can be determined in finite time using only the outputs. Mathematically, a system is observable if the observability matrix, which is constructed from matrices A and C has full rank. This means that the system's states can be reconstructed from its outputs.
Controllability (A, B):
Controllability, on the other hand, refers to the ability to move the system from any initial state to any final state within a finite period, using appropriate control inputs. A system is deemed controllable if, for any initial and final states, there exists a control input sequence that will transition the system from the initial to the final state in finite time. Mathematically, a system is controllable if the controllability matrix, constructed from matrices A and B, has full rank. This ensures that the control inputs can influence all states of the system.
Transformers and Softmax Self-Attention:
The article provides a concise overview of Transformers, describing their architecture with self-attention blocks and Multilayer Perceptron (MLP) blocks. The focus is on Transformers with a single self-attention block and MLP block, where the MLP block represents the identity function. The parameters of the self-attention block, particularly the softmax self-attention, are explained.
Causally masked Transformers are introduced, where tokens are treated as indexed by time. The paper drops tokens not observed at each timestep. The self-attention block in the causally masked context is detailed, and the concept of Transformer Filter is introduced. The tokens in this context are embeddings of state estimates and observations, generated recursively by the Transformer Filter. Notably, the Transformer Filter coincides with the Kalman Filter when H (history length) is 1.
Overall, this section provides a solid foundation for understanding the problems addressed in the article and introduces essential concepts such as Kalman Filtering, Linear-Quadratic-Control, and the architecture of Transformers with self-attention blocks. If you have specific questions or need further clarification on any part, feel free to let me know.
Gaussian Kernel Smoothing via Softmax Self-Attention:
This section presents the first major result of the paper, demonstrating that the class of Transformers studied is capable of representing a Gaussian kernel smoothing estimator. Here's a breakdown:
Theorem 1 - Representing Gaussian Kernel Smoothing:
The theorem establishes that a Transformer can represent a Gaussian kernel smoothing estimator. Given data {zi} and a query point z, the Gaussian kernel smoothing estimator outputs a linear combination of the data, weighted by the closeness of each data point to the query point, determined by a fixed covariance matrix Σ. The theorem quantifies this representation using a softmax self-attention block. The proof introduces a nonlinear embedding map φ and matrices M and A, providing a mathematical foundation for the representation.
Filtering and Transformer Implementation:
The subsequent part of the article transitions into the main question: "Can a Transformer implement the Kalman Filter?" Recognizing the complexity of a Transformer as a nonlinear function, the focus shifts to an approximation-theoretic question. The article proposes a one-layer Transformer, called the Transformer Filter, with a self-attention block that takes past state estimates and observations as input and generates state estimates.
Theorem 2 - Approximation of Kalman Filter by Transformer:
The theorem answers the approximation-theoretic question, showing that for any ε > 0, there exists a Transformer (specifically, the Transformer Filter) that generates state estimates ε-close to the Kalman Filter's estimates uniformly in time. The proof involves demonstrating that the state estimates of the Transformer Filter are close to those of the Gaussian kernel smoothing estimator, which, in turn, is represented by a Transformer. The mathematical details involve careful considerations of parameters such as β and ε1.
Review of Control Section:
This section focuses on the application of the Transformer Filter in control scenarios and its comparison to the Kalman Filter within the Linear-Quadratic-Gaussian (LQG) framework. Here's a breakdown:
Objective and Challenges:
The central question addressed is whether the Transformer Filter can be employed in place of the Kalman Filter in LQG control. However, due to the approximate nature of the Transformer representation of the Kalman Filter, the goal is not to implement the LQG controller exactly. Instead, the focus is on guaranteeing that the closed-loop dynamics induced by the Transformer closely approximate those generated by the LQG controller. This poses challenges as deviations in state estimates can lead to significant differences in control actions, and the stability of the closed-loop system needs to be analyzed.
The Linear-Quadratic-Gaussian (LQG) controller represents an advanced control strategy that integrates three pivotal concepts from control theory: linearity, quadratic cost, and Gaussian noise, tailored for systems with linear dynamics under the influence of Gaussian noise, optimizing a performance criterion framed by a quadratic cost function (El Khaldi et al., 2022). Below is an elucidation of the core components that underpin the LQG controller:
1. Linear (L): It operates under the premise that the system exhibits linear behavior, describable through linear equations. This foundational assumption of linearity streamlines the controller's analysis and design, rendering it versatile across a broad spectrum of engineering applications.
2. Quadratic (Q): The controller's optimization criterion or performance index is sculpted as a quadratic function involving the state variables and control inputs. The quadratic cost function is meticulously crafted to include terms that penalize both the deviation from the desired system state and the overutilization of control inputs, thus harmonizing system performance with the conservation of energy or control effort.
3. Gaussian (G): The design principle of the controller presupposes that the noise impacting the system, whether in the process or measurement phase, adheres to a Gaussian distribution. This probabilistic model of noise enables the employment of statistical methods to forecast and mitigate the noise's impact on the system.
Employing the Kalman Filter for state estimation, the LQG controller achieves an optimal state estimate amidst noise, subsequently deriving a control action that minimizes the quadratic cost function. This process adeptly balances the dual objectives of sustaining system performance and minimizing control effort amidst uncertainties (El Khaldi et al., 2022).
The inquiry into the feasibility of substituting the Kalman Filter with a Transformer Filter within the LQG control schema aims to assess if the Transformer can deliver state estimates with the requisite accuracy for effective LQG controller operation. Given the Transformer's adeptness at managing complex, nonlinear relations, this exploration into its integration into LQG control contemplates the possibility for improved performance in scenarios where the conventional linear paradigms falter, albeit with an acknowledgment of the inherent challenges in precisely emulating the LQG controller's behavior due to the approximate nature of the Transformer's functionality (El Khaldi et al., 2022).
Theorem 3 - Approximation of LQG Controller by Transformer:
The theorem establishes that, for any ε > 0, there exists a Transformer Filter that generates states ε-close to those produced by the LQG controller uniformly in time. The proof involves demonstrating that the closed-loop dynamics induced by the Transformer Filter, despite being nonlinear, remain stable.
Key Aspects of the Proof:
1. Stability Analysis: The proof involves analyzing the stability of the closed-loop dynamics. It emphasizes that the nonlinearity and memory in the closed-loop system are encapsulated in the variables {ηt}t≥0.
2. Matrix A Stability: Matrix A representing the closed-loop dynamics is proven to be stable, reinforcing the stability of the overall system.
3. Parameter Definitions: Parameters such as ε1, β, C, κ, M, and Θ are introduced and defined, illustrating the complexity of the analysis.
Interesting Consequence:
The section concludes by noting an interesting consequence of the result: the controller induced by the Transformer Filter is weakly stabilizing, meaning that, in the absence of disturbances, the states generated by the controller will eventually be confined to a ball of radius ε centered at the origin.
Why Approximate a Kalman Filter with a Transformer?
In the study conducted by Goel and Bartlett (2023), the potential of Transformer architectures to serve as alternatives to the traditional Kalman Filter is explored, revealing several advantages and novel approaches for state estimation and control within linear dynamical systems. This research underscores the significance of employing Transformer architectures over traditional Kalman Filters for enhancing system performance and efficiency.
Enhanced Management of Nonlinear Dynamics:
Conventional Kalman Filter Limitations: The traditional Kalman Filter, while effective in linear scenarios with Gaussian noise, struggles with nonlinear systems. Its nonlinear extension, the Extended Kalman Filter, relies on linearization around current estimates, which may not yield optimal results in highly nonlinear environments.
Transformer Advantages: Due to their deep learning architecture, Transformers inherently possess the capability to address nonlinear dynamics directly, bypassing the need for linearization. This direct approach to nonlinearities could potentially lead to improved performance in systems characterized by significant nonlinear behavior (Goel and Bartlett, 2023).
Advancements in Parallel Processing:
Drawbacks of Traditional Kalman Filter: The sequential data processing inherent to Kalman Filters imposes substantial computational burdens, particularly for large state spaces or voluminous data batches.
Transformers' Efficiency: By exploiting contemporary GPU technologies, Transformers enable parallel processing of data, substantially reducing computation times and enhancing efficiency for real-time processing or large-scale data handling needs (Goel and Bartlett, 2023).
Adaptability and Flexibility:
Traditional Kalman Filter Challenges: The efficacy of the Kalman Filter is closely tied to the precision of model parameters and noise statistics. Misestimations in system dynamics or noise characteristics can significantly impair its performance.
Transformers' Edge: Transformers exhibit the ability to learn from data, offering greater adaptability to varied system dynamics and noise profiles without the necessity for explicit model parameterization. This adaptability is particularly beneficial in scenarios where precise model parameters or noise statistics are challenging to ascertain (Goel and Bartlett, 2023).
Scalability:
Kalman Filter Limitations: Extending the Kalman Filter to manage very large state spaces can be challenging due to the computational and memory demands of its matrix operations.
Transformers' Capability: The design of Transformers facilitates scalability to extensive state spaces, leveraging advancements in deep learning optimizations and hardware acceleration. This scalability renders them suitable for complex systems with high-dimensional data (Goel and Bartlett, 2023).
Integration with Diverse Data Sources and Modalities:
Conventional Kalman Filter Limitations: Incorporating multiple data sources or modalities into the Kalman Filter framework can be complex and often necessitates custom adaptations.
Transformers' Versatility: Designed to handle various data types and modalities, Transformers are particularly adept at integrating diverse data sources, such as textual, visual, and sensor data. This capability allows for more robust state estimation and control strategies (Goel and Bartlett, 2023).
The exploration of Transformer architectures in the context of state estimation and control systems, as detailed by Goel and Bartlett (2023), marks a significant advancement in the field. While the application of Transformers instead of the Kalman Filter remains an area of ongoing research, the potential benefits in terms of adaptability, computational efficiency, and the ability to handle nonlinearities and high-dimensional data signal a promising direction for future developments in control theory and artificial intelligence.
Why not use an Extended Kalman Filter (EKF) to address nonlinearities?
The Extended Kalman Filter (EKF) and Transformer architectures present distinct methodologies for addressing nonlinear dynamics in dynamical systems, each bringing its unique set of strengths and weaknesses to the forefront. Below is an examination of the notable advantage attributed to the EKF, juxtaposed with the capabilities of Transformers, supplemented by internal citations to highlight their foundational principles and comparative advantages.
Pro of EKF: Modeling Nonlinearities as Linearities at Small Intervals
Grounded in the principle that nonlinear system dynamics can be linearized over small intervals, the EKF extends the linear framework of the Kalman Filter to nonlinear systems through linearization around current estimates (Kalman, 1960). This method provides a mathematically coherent strategy to manage nonlinearities, leveraging the established properties of linear systems. Such an approach renders the EKF adaptable and potent across a spectrum of applications marked by the presence of nonlinear dynamics but not dominated by them (Ribeiro & Ribeiro, 2004).
In contrast to the EKF, Transformers are intrinsically designed to handle nonlinearities due to their deep learning architecture. They bypass the need for linearization of system dynamics, as they are capable of directly modeling nonlinear relationships via self-attention mechanisms and nonlinear activation functions. This structural design enables Transformers to potentially discern and replicate more complex data patterns reflective of a system's inherent nonlinear behavior without relying on linear approximations (Goel & Bartlett, 2023).
Comparison:
Direct vs. Approximate Modeling: While the EKF's approximation of nonlinearities as linear within minimal intervals offers a computationally efficient and accurate solution for systems with mild nonlinear characteristics (Ribeiro & Ribeiro, 2004), it may fall short in capturing the entirety of highly complex nonlinear dynamics. Conversely, Transformers promises a more precise depiction of such dynamics through direct modeling, albeit with increased computational demands and extensive training data requirements (Goel & Bartlett, 2023).
Computational Complexity and Data Requirements: The linearization tactic employed by the EKF is less computationally intensive, thereby facilitating easier application in scenarios with limited computational resources (Ribeiro & Ribeiro, 2004). On the other hand, the data-driven learning attribute of Transformers positions them as a formidable tool for navigating complex nonlinearities, contingent on the availability of adequate computational capabilities and data (Goel & Bartlett, 2023).
In essence, the mathematical simplicity and operational efficiency of the EKF in approximating nonlinear dynamics as linear over concise intervals underscore its suitability for a broad array of applications with mild nonlinearities. This stands in contrast to Transformers, whose inherent ability to directly tackle nonlinear relationships offers a promising yet computationally demanding alternative for systems characterized by intricate nonlinear dynamics.
Note: EKF Computational Intensity
The Kalman Filter and EKF, designed to extend the linear Kalman Filter's capabilities to nonlinear systems through linearization at each timestep, can become computationally burdensome with increasing system size (Kalman, 1960). This burden is primarily due to the matrix operations required, which escalate in complexity with the dimensionality of the state space (Ribeiro & Ribeiro, 2004). The necessity for real-time or near-real-time processing in large systems compounds these challenges, making the EKF less viable in scenarios demanding rapid computation over extensive datasets.
Transformer Computational Intensity:
Transformers, in contrast, harness the parallel processing power of modern computational hardware, such as GPUs, enabling efficient handling of large-scale data and high-dimensional inputs (Vaswani et al., 2017). Their architecture, while computationally intensive during the training phase, facilitates a more manageable execution during inference, provided the model has been adequately trained on sufficient data to capture the system's dynamics accurately.
Comparative Insights:
In Small to Medium-Sized Systems: The operational efficiency of the EKF may surpass that of Transformers, given the latter's extensive computational and data requirements for training. The EKF's streamlined process for approximating nonlinear dynamics offers a practical solution for systems where real-time processing with limited computational resources is a priority (Ribeiro & Ribeiro, 2004).
For Large-Scale, Highly Nonlinear Systems: Transformers present a compelling alternative, capable of directly modeling complex nonlinear relationships without the need for linear approximations. This advantage is balanced by the significant computational resources required for model training, although parallel processing capabilities can mitigate these demands during inference (Vaswani et al., 2017).
Application-Specific Considerations: The decision between employing an EKF or a Transformer hinges on the application's unique requirements, including system size, complexity of dynamics, computational resource availability, and the necessity for real-time analytics.
In essence, while EKFs offer a methodologically sound approach for approximating nonlinear dynamics in smaller systems, Transformers provide a robust framework for analyzing large-scale data and complex interactions, albeit with considerable computational investment in the training phase. The selection of one approach over the other should be informed by the specific operational needs and constraints of the task at hand.
Conclusion:
In the ever-evolving landscape of scientific exploration, this journey into the realm of state estimation and control using Transformer architectures has provided valuable insights. As we delved into the intricacies of linear dynamical systems, the potential of Transformers emerged as an intriguing alternative to classical methods like the Kalman Filter.
As Albert Szent-Györgyi, the Hungarian biochemist and Nobel laureate, once wisely expressed, "In science, seeing what everyone else sees is not enough; you have to think what no one else has thought, about what everyone else is seeing." This sentiment resonates with the essence of scientific inquiry — the constant pursuit of new questions and novel approaches to existing challenges.
The study's exploration of Transformer applications in filtering and control not only adds a layer of computational efficiency but also opens doors to adaptability in handling nonlinearities. While traditional methods like the Kalman Filter remain stalwarts in the field, the quest for alternatives is a hallmark of scientific curiosity.
As we navigate the intersections of technology, artificial intelligence, lidar technology, and photogrammetry, the Transformer's foray into state estimation sparks curiosity and sparks contemplation about the future landscape of control systems. This journey reminds us that in the scientific pursuit, questioning the conventional is an essential step toward innovation.
I genuinely hope you have learned something and thank you for reading; I really appreciate it. If you like the article please share and subscribe!
References:
El Khaldi, L., Sanbi, M., Saadani, R., & Rahmoune, M. (2022). LQR and LQG-Kalman active control comparison of smart structures with finite element reduced-order modeling and a Monte Carlo simulation. *Frontiers in Mechanical Engineering, 8*, 912545. doi: 10.3389/fmech.2022.912545
Goel, G., & Bartlett, P. (Year, Month Day). Can a Transformer Represent a Kalman Filter? arXiv preprint arXiv:2312.06937 [cs.LG]. Retrieved from https://arxiv.org/abs/2312.06937
(or https://arxiv.org/abs/2312.06937v2 for this version)
DOI: 10.48550/arXiv.2312.06937
Kalman, R. E. (1960). A New Approach to Linear Filtering and Prediction Problems. Journal of Basic Engineering, 82(1), 35–45. doi:10.1115/1.3662552
Ogata, K. (2010). Modern Control Engineering (5th ed.). Prentice Hall.
Ribeiro, M., Ribeiro, I., 2004. Kalman and Extended Kalman Filters: Concept, Derivation and Properties.
About the Author
Daniel Rusinek is an expert in LiDAR, geospatial, GPS, and GIS technologies, specializing in driving actionable insights for businesses. With a Master's degree in Geophysics obtained in 2020, Daniel has a proven track record of creating data products for Google and Class I rails, optimizing operations, and driving innovation. He has also contributed to projects with the Earth Science Division of NASA's Goddard Space Flight Center. Passionate about advancing geospatial technology, Daniel actively engages in research to push the boundaries of LiDAR, GPS, and GIS applications.